Le corps noir
Message de la lumière :
• Atomes et lumière
• Les prémices
• La controverse
• Naissance d'une science
• Les types spectraux
• Rayonnement électromagnétique
• Le corps noir
Rayonnement du corps noir
les caractéristiques d'un rayonnement sont liées aux conditions physico-chimiques de la matière : composition, pression, température...
La température est la mesure de l'agitation (l'énergie cinétique) des constituants d'un milieu. Elle se mesure en température absolue sur l'échelle Kelvin (K), le point zéro y désignant une agitation cinétique nulle. Elle vaut la température Celsius (°C), augmentée de 273.15 :
T(K) = T(°C) + 273.15
Dans le cas d'un corps absolument opaque, parfaitement isolé et à température constante, la distribution spectrale est strictement liée à la seule température. Ce cas théorique est appelé « corps noir ». En première approximation, une étoile peut être assimilée à un corps noir (presque) parfait ; la perte en énergie rayonnée restant négligeable devant celle contenue à l'intérieur de l'étoile.
Les lois déterminant l'état de la matière dans un corps noir s'appuient sur des études théoriques et expérimentales. Elles définissent :
- la distribution de la luminance en fonction de la longueur d'onde (loi de Planck) ;
- la longueur d'onde à laquelle la luminance est maximale (loi de Wien) ;
- l'énergie totale du rayonnement (loi de Stefan).

Portraits de Max PLANCK (1858 - 1947), Wilhelm WIEN (1864 - 1928) et Josef STEFAN (1838 - 1893).
La loi de Stefan
en 1879, à partir de résultats expérimentaux, Josef STEFAN (1838 - 1893) détermine une loi empirique décrivant que l'énergie totale (E) émise par seconde et par unité de surface (S) d'un corps noir est proportionnelle à la puissance quatre de sa température (T) :
E = S σ T4
où σ est la constante de Stefan et vaut : 5.67 × 10-8 W m-2 K-4.
En considérant une étoile sous la forme d'une sphère rayonnant comme un corps noir, cette relation devient :
E = 4π R2 σ T4, avec S = 4π R2.
Pour deux étoiles présentant la même température de surface, la plus grosse émettra plus d'énergie. Pour une variation double de la température, une étoile émettra seize fois plus d'énergie à rayon égal. La loi de Stefan permet donc de retrouver la dimension d'une étoile, il faut cependant mesurer la puissance de l'énergie sur toute la bande spectrale, une étoile émettant bien au-delà du spectre visible.
En 1884, Ludwig BOLTZMANN (1844 - 1906) apportera une confirmation théorique en retrouvant la loi de Stefan à partir des relations fondamentales de la thermodynamique. Pour cette raison, cette relation est également connue sous le nom de loi de Stefan-Boltzmann.
La loi de Wien
Si cette relation température-couleur permet de retrouver facilement la température d'un corps lorsque l'on a déterminé le maximum d'émission, à l'inverse, il est également possible de découvrir le maximum d'émission à partir d'une température.
Ex : la température du corps humain est de 37.5 °C, soit environ 310 K. On a donc :
λmax = (2.90 × 10-3) / 310 = 9.35 × 10-6 m ou 9350 nm.
Le maximum d'émission du corps humain se fait donc dans l'infrarouge.
en analysant des spectres de corps noirs à différentes températures, Wilhelm WIEN (1864 - 1928) découvre, en 1893, que la distribution de leurs émissions passe par un maximum, ce dernier étant inversement proportionnel à la température. Plus la température devient élevée, plus la longueur d'onde du pic d'émission diminue (la fréquence et l'énergie augmentent). Cette relation « température-couleur » s'exprime ainsi :
λmax = (2.90 × 10-3) / T
avec la longueur (λ) et la température (T) exprimées dans le Système International d'unités.
Pour le Soleil, le maximum d'émission se situe vers 500 nm (lumière jaune-verte), sa température de surface vaut : T = (2.90 × 10-3) / (0.50 × 10-6) = 5 800 kelvins.
La loi de Planck
Max PLANCK (1858 - 1947) est l'auteur d'une théorie des quanta d'énergie (1900) et l'applique avec succès à l'explication du rayonnement du corps noir. Il suppose que l'échange d'énergie entre matière et rayonnement se fait de façon discontinue, par quanta. Ces quanta (ε) sont proportionnels aux fréquences (ν) du rayonnement :
ε = hν
avec h, une constante de proportionnalité (constante de Planck) valant : 6.62 × 10-34 joules·s-1.
La loi de Planck permet de donner la distribution de l'énergie selon la longueur d'onde (ou couleur). Les courbes décrivant cette distribution se retrouvent toujours sous une même forme « en cloche » et incluses les unes dans les autres. Pour chaque longueur d'onde, la luminance augmente avec la température.
Avec son quantum d'énergie introduit de façon arbitraire, cette théorie de quantification de l'énergie, vue comme simple artifice de calcul à ses débuts, permet d'intégrer les lois précédentes et deviendra vite une pièce maîtresse de la mécanique quantique.
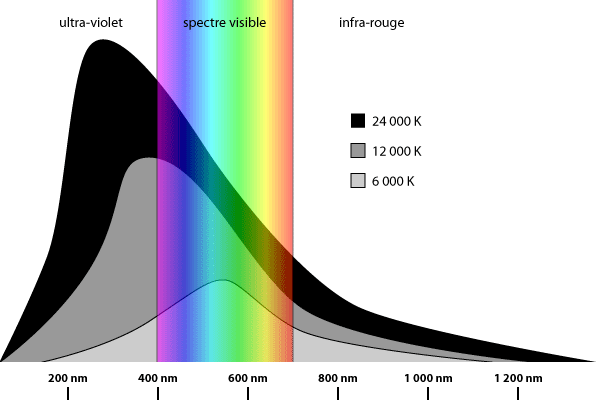
Schématisation de la distribution de l'énergie de corps noirs à trois températures différentes.
En fonction de la température et de la longueur d'onde, le schéma ci-dessus montre pour trois étoiles :
- la forme caractéristique « en cloche » de la distribution de luminance (loi de Planck) ;
- le déplacement du pic d'émission (loi de Wien) ;
- l'énergie totale rayonnée représentée par l'aire sous la courbe (loi de Stefan).